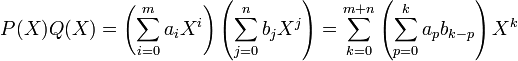Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


Definición algebraica
Polinomios de una variable
Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como  o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero, para n > 0, entonces un polinomio, P, de grado n en la variable x es un objeto de la forma
El polinomio se puede escribir más concisamente usando sumatorios como
Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado. Siendo x un símbolo llamado indeterminada.
[editar] Polinomios de varias variables
Los polinomios de varias variables son similares a los de una variable. La diferencia es que en ellos cada uno de los monomios puede contener más de una letra de variable. Por ejemplo:
Son monomios de varias variables. Más en detalle el último de ellos scriptstyle 4uv^2t es un momonio de tres variables
(ya que en él aparecen tres letras x, y y z), el coeficientes es 4, y los exponentes son 1, 2 y 1, ya que xy2z = x1y2z1.
Operaciones con polinomios
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un polinomio por los términos del otro polinomio y se simplifican los monomios semejantes, posteriormente. Por ejemplo:
Para poder realizar eficazmente la operación tienes que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:
Puede comprobarse que para polinomios no nulos se satisface la siguiente relación entre el grado de los polinomios  y
y  y el polinomio producto
y el polinomio producto  :
:
(*)
Puesto que el producto de cualquier polinomio por el polinomio nulo es el propio polinomio nulo, se define convencionalmente que  (junto con la operación
(junto con la operación  ) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
12683