
Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


TeorÍa de Conjuntos
NOCION INTUITIVA DE CONJUNTO
Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre si, que se llaman elementos del mismo.
Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
Ejemplos de conjuntos:
-
- Æ : el conjunto vacío, que carece de elementos.
- N: el conjunto de los números naturales.
- Z: el conjunto de los números enteros.
- Q : el conjunto de los números racionales.
- R: el conjunto de los números reales.
- C: el conjunto de los números complejos.
Se puede definir un conjunto:
-
- por extensión, enumerando todos y cada uno de sus elementos.
- por comprensión, diciendo cuál es la propiedad que los caracteriza.
Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión,
o su propiedad característica, si se define por comprensión. Por ejemplo:
-
- A := {1,2,3, ... ,n}
- B := {pÎ Z | p es par}
Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B),
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B.
Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
Para cualquier conjunto A se verifica que ÆÍ A y A Í A;
B Í A es un subconjunto propio de A si A ¹ Æ y B ¹ A.
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A). Ejemplos:
Si a Î A entonces {a} ÎÃ (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.
OPERACIONES ENTRE CONJUNTOS
Dados dos conjuntos A y B, se llama diferencia al conjunto A - B := {a Î A | a Ï B}.
Asimismo, se llama diferencia simétrica entre A y B al conjunto A D B := (A - B) È (B - A).
Si A Î Ã (U), a la diferencia U - A se le llama complementario de A respecto de U,
y se denota abreviadamente por A' (U se supone fijado de antemano).
Es fácil ver que si A y B son subconjuntos cualesquiera de U se verifica:
-
- Æ ' = U .
- U ' = Æ .
- (A')' = A .
- A Í B Û B' Í A' .
- Si A = { x Î U | p(x) es una proposición verdadera} entonces A' = { x Î U | p(x) es una proposición falsa}.
Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
es decir: A È B := { x | x Î A Ú x Î B}.
Se llama intersección de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B,
es decir: A Ç B := {x | x Î A Ù x Î B}.
Si A y B son subconjuntos de un cierto conjunto universal U, entonces es fácil ver que A - B = A Ç B'.
En este caso, la llamadas operaciones booleanas (unión e intersección) verifican las siguientes propiedades :
| PROPIEDADES | UNION | INTERSECCION |
| 1.- Idempotencia | A È A = A | A Ç A = A |
| 2.- Conmutativa | A È B = B È A | A Ç B = B Ç A |
| 3.- Asociativa | A È ( B È C ) = ( A È B ) È C | A Ç ( B Ç C ) = ( A Ç B ) Ç C |
| 4.- Absorción | A È ( A Ç B ) = A | A Ç ( A È B ) = A |
| 5.- Distributiva | A È ( B Ç C ) = ( A È B ) Ç ( A È C ) | A Ç ( B È C ) = ( A Ç B ) È ( A Ç C ) |
| 6.- Complementariedad | A È A' = U | A Ç A' = Æ |
Además de éstas, se verifican también las siguientes propiedades:
-
- A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
- A È U = U , A Ç U = A ( elemento universal ).
- ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de Morgan ).
Dados dos conjuntos A y B, se define el producto cartesiano de ambos como el conjunto de pares ordenados:
Dos pares (a,b) y (c,d) de A ´ B son iguales si a = c y b = d; análogamente, dados cuatro conjuntos A,B,C,D se verifica
Se llama grafo relativo a A ´ B a todo subconjunto G Í A ´ B.
Dado un grafo G relativo a A ´ B, se llama proyección de G sobre A al conjunto
Análogamente se define la proyección ProyBG de G sobre B.
Por último, los conceptos anteriores pueden generalizarse a familias de conjuntos.
Si para cada elemento i de un conjunto (de índices ) I se tiene un conjunto Ai , entonces se define el conjunto { Ai : i Î I }
y se denomina familia de conjuntos indicada por I. También se suele denotar por { Ai } i Î I .
De forma análoga se define una familia de elementos ( ai ) i Î I .
Dada una familia de conjuntos { Ai } i Î I se definen:
-
- È i ÎI Ai := { a : a Î Ai , $ i Î I }
- Ç i Î I Ai := { a : a Î Ai , " i Î I }
- Õ i Î I Ai := { (ai) : ai Î Ai , " i Î I }
Las propiedades de la unión e intersección siguen siendo válidas para familias de conjuntos, y en particular las leyes de Morgan :
Los conjuntos de suelen representar gráficamente mediante "diagramas de Venn", con una línea que encierra a sus elementos.
Así, todas las operaciones entre conjuntos se pueden representar gráficamente con el fin de obtener una idea más intuitiva.
A Í B
A È B
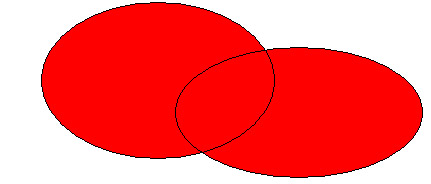
A Ç B
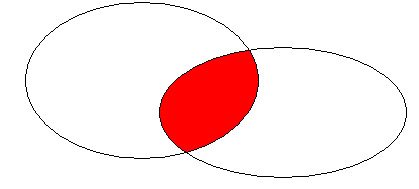
A - B
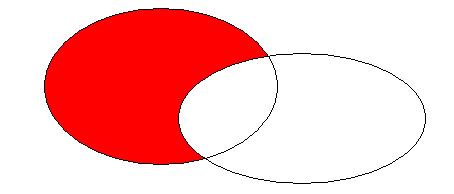
A D B
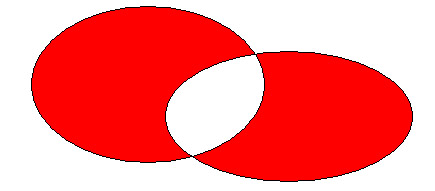
12680